viernes, 1 de julio de 2011
recordando; traslación de función
Sea
y = f (x) una función.·
La función y = f (x - h) es la función f (x) trasladada h unidades en horizontal. Sih
>0 el desplazamiento es hacia la derecha y si h<0 es hacia la izquierda.y
= sin( x - p ) es la función y = sin x desplazada p unidades hacia la derechay
= sin( x - p )y
= sin x·
La función y = f (x) + k es la función f (x) desplazada k unidades en vertical. Sik>0
el desplazamiento es hacia arriba y si k<0 el desplazamiento es hacia abajo.0 1.25 2.5 3.75 5 6.25
1
0.5
0
-0.5
-1
x
y
0 1.25 2.5 3.75 5 6.25
1
0.5
0
-0.5
-1
x
y
y
= 2x (negro) y = 2x + 2 (rojo)·
La función y = f (x - h) + k es la función f (x) desplazada k unidades en vertical yh
Si somos capaces de determinar los desplazamientos, podremos dibujar funciones más o
menos complejas desplazando funciones elementales.
Las parábolas:
Sea
unidades en horizontal.y = ax2 la parábola elemental de vértice (0,0) y eje x = 0. La parábolay
= a(x - p)2 + q es la parábola elemental trasladada. Vértice (p ,q)y
= x2 y = (x - 1) 2 +1 V(1,1)-5 -2.5 0 2.5 5
10
5
0
-5
-10
x
y
Para hallar los parámetros de desplazamiento respecto a la parábola elemental basta
hallar el vértice en la parábola
y = ax2 + bx + c÷ ÷ø
ö
ç çè
æ -
-
-
=
a
b ac
a
b
V
4
4
,
2
2
Las hipérbolas
La hipérbola elemental es
x
a
y
= . Cualquier hipérbola de la formapx q
mx n
y
+
+
=
expresarse de la forma
x h
a
y
-
=
respecto a la hipérbola elemental.
3 2
2 1
( )
puedek+siendo h y k los parámetros de desplazamiento-
+
=
x
x
f x
hacemos la división 2
2
3
y de resto
3
7
. Como:
( )
( )
( )
( )
( )
x +1 : (3x - 2) y obtenemos de cocienteq x
r x
c x
q x
p x
= +
3 2
3
7
2
3
3 2
2 1
( )
siendo c(x) el cociente y r(x) el resto-
= +
-
+
=
x x
x
f x
Para que el denominador de la fracción algebraica sea 1 dividimos numerador y
denominador por 3:
3
2
9
7
2
3
3
3 2
3
1
3
7
2
3
3 2
3
7
2
3
3 2
2 1
( )
-
= +
-
×
= +
-
= +
-
+
=
x
x x x
x
f x
Nuestra función es la parábola
x
9
7
desplazada 2/3 en horizontal y 3/2 en vertical
y
= 1/ x y = 1/(x - 2) + +5-2 -1 0 1 2
20
10
0
-10
-20
x
y
encuentra la función inversa y gráfica
Se llama función inversa o reciproca de f a otra función f−1 que cumple que:
Si f(a) = b, entonces f−1(b) = a.

Podemos observar que:
El dominio de f−1 es el recorrido de f.
El recorrido de f−1 es el dominio de f.
Si queremos hallar el recorrido de una función tenemos que hallar el dominio de su función inversa.
Si dos funciones son inversas su composición es la función identidad.
f o f -1 = f -1 o f = x
Las gráficas de f y f -1 son simétricas respecto de la bisectriz del primer y tercer cuadrante.

Hay que distinguir entre la función inversa, f−1(x), y la inversa de una función,  .
.
Cálculo de la función inversa
1Se escribe la ecuación de la función con x e y.
2Se despeja la variable x en función de la variable y.
3Se intercambian las variables.
Calcular la función inversa de:
como se calcula el crecimiento de población
El crecimiento de la población es el resultado de la dinámica demográfica, es decir, de la interrelación entre los nacimientos, las defunciones y migraciones ocurridas en un determinado período. La población aumenta por efecto de los nacimientos, y de las inmigraciones, y disminuye a causa de las defunciones y emigraciones.
Si la suma de los nacimientos y las inmigraciones es mayor que la suma de las muertes y las emigraciones, entonces la población experimenta un crecimiento. Contrariamente da como resultado un decrecimiento poblacional.
como se calcula el interés compuesto
- Paso 1
Ahora bien, comencemos por lo primero: El interés compuesto es aquel monto obtenido por el préstamo, cuando el dinero que se recibe del capital inicial pasa a ser parte de ese mismo capital al final del primer período de tiempo.
La diferencia fundamental que existe entre el interés simple y el interés compuesto consiste en que el interés simple liquida los intereses cada periodo y se pagan inmediatamente.
En el interés compuesto los intereses liquidados se acumulan al capital para formar un nuevo capital denominado monto, y sobre este monto se calculan los nuevos intereses del siguiente periodo.
La diferencia fundamental que existe entre el interés simple y el interés compuesto consiste en que el interés simple liquida los intereses cada periodo y se pagan inmediatamente.
En el interés compuesto los intereses liquidados se acumulan al capital para formar un nuevo capital denominado monto, y sobre este monto se calculan los nuevos intereses del siguiente periodo.
- Paso 2
Recoge algunos datos básicos sobre el préstamo o inversión para el cual quieres calcular el interés compuesto. Necesitarás saber el capital inicial con el que comenzaste, la tasa de interés anual pagada, y el número de años que quieres calcular de interés.
Fórmula del interés compuesto
- Paso 3
Utiliza la fórmula S = P (1+i)n, en la que:
S = Capital final
p = Capital inicial
i = Tasa de interés
n = Número de períodos
p = Capital inicial
i = Tasa de interés
n = Número de períodos
· Paso 4
Comienza trabajando con la parte de la fórmula que está entre paréntesis. Suma 1 a la tasa de interés anual. Luego, toma ese número y elévalo a la potencia del número de años para los cuales quieres calcular el interés.
· Paso 5
Toma el resultado que obtienes del paréntesis y multiplícalo por el capital inicial. El resultado es cuánto dinero resultará del interés compuesto en el período de años que hayas especificado
Lee mas en: http://www.enplenitud.com/nota.asp?notaid=10242#ixzz1QqCWYfHF
Descarga libros gratis en http://www.enplenitud.com/libros
ecuación de la parábola
Ecuación reducida de la parábola

Dada la parábola  , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.


Dada la parábola  , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.

derivada
la derivada se representa cómo una función que cambia (valor de la variable dependiente) a medida que su entrada (valor de la variable independiente) cambia. En términos poco rigurosos, una derivada puede ser vista como cuánto está cambiando el valor de una función en un punto dado (o sea su velocidad de variación); por ejemplo, la derivada de la posición de un vehículo con respecto al tiempo, es la velocidad instantánea con la cual el vehículo está viajando.
La derivada de una función es un valor de entrada dado que describe la mejor aproximación lineal de una función cerca del valor de entrada. Para funciones de valores reales de una sola variable, la derivada en un punto representa el valor de la pendiente de la recta tangente a la gráfica de la función en dicho punto. En dimensiones más elevadas, la derivada de una función en un punto es la transformación lineal que más se aproxima a la función en valores cercanos de ese punto. Algo estrechamente relacionado es el diferencial de una función.
El proceso de encontrar una derivada es llamado diferenciación. El teorema fundamental del cálculo dice que la diferenciación es el proceso inverso de la integración en funciones continuas.
La derivada de una función es un valor de entrada dado que describe la mejor aproximación lineal de una función cerca del valor de entrada. Para funciones de valores reales de una sola variable, la derivada en un punto representa el valor de la pendiente de la recta tangente a la gráfica de la función en dicho punto. En dimensiones más elevadas, la derivada de una función en un punto es la transformación lineal que más se aproxima a la función en valores cercanos de ese punto. Algo estrechamente relacionado es el diferencial de una función.
El proceso de encontrar una derivada es llamado diferenciación. El teorema fundamental del cálculo dice que la diferenciación es el proceso inverso de la integración en funciones continuas.
buscar la ecuación de la parábola
Ecuación reducida de la parábola

Dada la parábola  , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.


Dada la parábola  , calcular su vértice, su foco y la recta directriz.
, calcular su vértice, su foco y la recta directriz.

investigar las propiedades de las curvas en una función
se definen como los conjuntos de puntos en el espacio de combinaciones de bienes para los que la satisfacción del consumidor es idéntica, es decir que para todos los puntos pertenecientes a una misma curva, el consumidor no tiene preferencia por la combinación representada por uno sobre la combinación representada por otro. La satisfacción del consumidor se caracteriza mediante la función de utilidad en la que las variables son las cantidades de cada bien representadas por el valor sobre cada eje.
Existen discrepancias entre autores sobre si la continuidad, derivabilidad y convexidad de dichas curvas están garantizadas y ello tiene fuertes implicaciones en al discusión de la existencia o no de puntos de equilibrio. Desde un punto de vista matemático la discusión implica el axioma de elección
Existen discrepancias entre autores sobre si la continuidad, derivabilidad y convexidad de dichas curvas están garantizadas y ello tiene fuertes implicaciones en al discusión de la existencia o no de puntos de equilibrio. Desde un punto de vista matemático la discusión implica el axioma de elección
función racionales asíntotas
ASINTOTA es la recta a la cual se aproxima la función, sin llegar a tocarla
ASÍNTOTA HORIZONTAL: Condición: El grado del numerador tiene que ser
Es el límite de la función cuando x
≤ que el denominador± ∞Forma de hallarla: 1º) Se halla la asíntota lim f(x) cuando
x → +∞, lim f(x) cuando x → −∞2º) Se hallas los límites laterales
Ej:
1
3
2
2
+
=
x
y x
1
3
lim lim 3 32
2
2
2
= =
+
x
x
x
xAsíntota horizontal y = 3x
→ ∞ x → ∞2º
x
→ +∞f(x) 3
- (por debajo de la asíntota, no llega a 3)Una función tiene como máximo dos
f(x) 3- (por debajo de la asíntota, no llega a 3)La función puede cortar a las A. H.
ASÍNTOTA VERTICAL La recta x = a es asíntota vertical si al tender x a el límite de la función es
± ∞Forma de hallarla: 1º) Las A. Verticales serán los
2º) Se hallan los límites laterales
Ej:
valores que anulan al denominador pero no al numer.x
y
= 1 1º) Denominador = 0; Asíntota vertical x = 02º)
→ +∞
→
+( )
0
f x
x
→ −∞
→
−( )
0
f x
x
La función puede tener infinitas asíntotas verticales. Una función no corta nunca a la asíntota vertical
ASÍNTOTA OBLICUA Condición: El grado del numerador tiene que ser = al grado del denominador + 1
La asíntota oblicua es de la forma
y = mx + n (hay que hallar m y n)Forma de hallarla:
→ ∞
=
x
x
m
lim f ( x )→ ∞
= −
n
xlim( f (x) mx)Ej:
x
y x
2 +1=
→ ∞
= = =
+
=
+
= =
x
m
x
x
x
x
x x
x
x
m f x
1
lim ( ) lim
2
2
2
2
lim 1 lim 1, , 12lim( ( ) ) lim 1 1 lim 1 lim 1 0
2 2 2
= =
+ −
= ⎟
⎟⎠
⎞
⎜ ⎜⎝
⎛
−
+
= − =
x x
x x x
x
n f x mx x
y = mx + n; y = 1x + 0 ;
n=0y = x Asíntota OblicuaPara saber por qué lado va se sustituye en la curva y en la asíntota el mismo valor: en el ejemplo anterior
x =2 en la asíntota y = 2 (2, 2); en la curva
2
5
2
2
2'52 1= =
+
y
Igual se hace en el lado negativo. Cuando x = -2; en la asíntota (-2, -2). En la curva (-2, -2’5)
LÍMITES CUANDO
= (2, 2’5), La curva va por encimax → ∞Si es un polinomio, se halla el límite del término de mayor grado
Si es una fracción, se halla el límite de los dos términos de mayor grado (numerador y denominador)
grafica las siguientes expresiones
este es un ejemplo:
la primera tenía: y = x + 3
tengo los valores: 2, +1 , 0 , -1 , -2 e hize lo siguiente:
y = (2) + 3 = 5
y = (1) + 3 = 4
y = (0) + 3 = 3
y = (-1) + 3 = 2
y = (-2) + 3 = 1
Mi problema es que no se como sustituir las siguientes 2 y cómo es el orden :
a) y = 2x + 1
b) y = -3x + 2
c) y = -2x+3
la primera tenía: y = x + 3
tengo los valores: 2, +1 , 0 , -1 , -2 e hize lo siguiente:
y = (2) + 3 = 5
y = (1) + 3 = 4
y = (0) + 3 = 3
y = (-1) + 3 = 2
y = (-2) + 3 = 1
Mi problema es que no se como sustituir las siguientes 2 y cómo es el orden :
a) y = 2x + 1
b) y = -3x + 2
c) y = -2x+3
la división de un polinomio entre un monomio
El objetivo de esta operacion es fundamentalmente obtener un polinomio, el cual esta formado a partir de los resultados de dividir cada uno de sus terminos entre el monomio que esta actuando como divisor. Se aplican en consecuencia todas las reglas del caso de division de mEn este caso, cada uno del los terminos del dividendo, que es un polinomio, sera divido entre el monomio que actua como divisoronomios
funciones polinomiales de 3 grado y 4 grado
Polinomio de grado 3:
f(x) = x3/5 + 4×2/5 - 7x/5 - 2 = 1/5 (x+5)(x+1)(x-2)
Polinomio de grado 4:
f(x) = 1/14 (x+4)(x+1)(x-1)(x-3) + 0.5
para qué sirve la derivada
Supongamos que tenemos una función y la llamamos  . La derivada de
. La derivada de  es otra función que llamaremos
es otra función que llamaremos  .
.
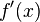 representa la pendiente de la recta tangente a la gráfica de
representa la pendiente de la recta tangente a la gráfica de  en el punto
en el punto  .
.
En términos geométricos, esta pendiente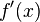 es «la inclinación» de la línea recta que pasa justo por encima del punto
es «la inclinación» de la línea recta que pasa justo por encima del punto 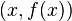 y que es tangente a la gráfica de
y que es tangente a la gráfica de  .
.
Al identificar dos puntos muy cercanos en la gráfica y al unirlos mediante una línea recta, una pendiente queda visualizada. Cuanto más cercanos sean los dos puntos que se unen por medio de la recta, la recta se parece más a una recta tangente a la gráfica y su pendiente se parece más a la pendiente de una recta tangente.
Notamos que esta pendiente coincide con la rapidez con que aumenta o disminuye el valor de la función en cada punto. Dicho de otra manera, si la pendiente en un punto es muy grande, entonces el valor de la función en ese punto crece (o decrece) muy deprisa; si la pendiente es muy pequeña, entonces el valor de la función crece (o decrece) muy despacio en ese punto.
Es decir, tanto la pendiente de la recta tangente como la rapidez de crecimiento (o decrecimiento) en un punto de una función
de una función  está dado por
está dado por 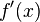 .
.
No todas las funciones poseen derivada. Desde el punto de vista geométrico esto se puede deber a varios motivos. Por ejemplo hay funciones donde se da el caso de que por un mismo punto pasan muchas rectas tangentes(por ejemplo la función valor absoluto en el punto 0) y no es posible definir de manera única la pendiente a la recta tangente. También se da el caso de que no se puede definir la pendiente a una recta tangente en una función que no es continua. Incluso hay funciones donde cualquier recta que pase por uno de sus puntos interseca en una infinidad de puntos muy cercanos y por tanto no hay recta tangente.
Las funciones que poseen derivada se llaman diferenciables.
Conocer la derivada de una función diferenciable por lo general resulta una tarea sencilla utilizando las técnicas de derivación desarrolladas por Gottfried Leibniz e Isaac Newton, las cuales permiten conocer las derivadas de muchas de las funciones de interés frecuente o bien, simplificar el trabajo para encontrar derivadas menos comunes.
 . La derivada de
. La derivada de  es otra función que llamaremos
es otra función que llamaremos  .
.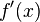 representa la pendiente de la recta tangente a la gráfica de
representa la pendiente de la recta tangente a la gráfica de  en el punto
en el punto  .
.En términos geométricos, esta pendiente
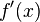 es «la inclinación» de la línea recta que pasa justo por encima del punto
es «la inclinación» de la línea recta que pasa justo por encima del punto 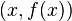 y que es tangente a la gráfica de
y que es tangente a la gráfica de  .
.Al identificar dos puntos muy cercanos en la gráfica y al unirlos mediante una línea recta, una pendiente queda visualizada. Cuanto más cercanos sean los dos puntos que se unen por medio de la recta, la recta se parece más a una recta tangente a la gráfica y su pendiente se parece más a la pendiente de una recta tangente.
Notamos que esta pendiente coincide con la rapidez con que aumenta o disminuye el valor de la función en cada punto. Dicho de otra manera, si la pendiente en un punto es muy grande, entonces el valor de la función en ese punto crece (o decrece) muy deprisa; si la pendiente es muy pequeña, entonces el valor de la función crece (o decrece) muy despacio en ese punto.
Es decir, tanto la pendiente de la recta tangente como la rapidez de crecimiento (o decrecimiento) en un punto
 de una función
de una función  está dado por
está dado por 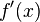 .
.No todas las funciones poseen derivada. Desde el punto de vista geométrico esto se puede deber a varios motivos. Por ejemplo hay funciones donde se da el caso de que por un mismo punto pasan muchas rectas tangentes(por ejemplo la función valor absoluto en el punto 0) y no es posible definir de manera única la pendiente a la recta tangente. También se da el caso de que no se puede definir la pendiente a una recta tangente en una función que no es continua. Incluso hay funciones donde cualquier recta que pase por uno de sus puntos interseca en una infinidad de puntos muy cercanos y por tanto no hay recta tangente.
Las funciones que poseen derivada se llaman diferenciables.
Conocer la derivada de una función diferenciable por lo general resulta una tarea sencilla utilizando las técnicas de derivación desarrolladas por Gottfried Leibniz e Isaac Newton, las cuales permiten conocer las derivadas de muchas de las funciones de interés frecuente o bien, simplificar el trabajo para encontrar derivadas menos comunes.
que es derivar
la derivada se representa cómo una función que cambia (valor de la variable dependiente) a medida que su entrada (valor de la variable independiente) cambia. En términos poco rigurosos, una derivada puede ser vista como cuánto está cambiando el valor de una función en un punto dado (o sea su velocidad de variación); por ejemplo, la derivada de la posición de un vehículo con respecto al tiempo, es la velocidad instantánea con la cual el vehículo está viajando.
La derivada de una función es un valor de entrada dado que describe la mejor aproximación lineal de una función cerca del valor de entrada. Para funciones de valores reales de una sola variable, la derivada en un punto representa el valor de la pendiente de la recta tangente a la gráfica de la función en dicho punto. En dimensiones más elevadas, la derivada de una función en un punto es la transformación lineal que más se aproxima a la función en valores cercanos de ese punto. Algo estrechamente relacionado es el diferencial de una función.
El proceso de encontrar una derivada es llamado diferenciación. El teorema fundamental del cálculo dice que la diferenciación es el proceso inverso de la integración en funciones continuas.
La derivada de una función es un valor de entrada dado que describe la mejor aproximación lineal de una función cerca del valor de entrada. Para funciones de valores reales de una sola variable, la derivada en un punto representa el valor de la pendiente de la recta tangente a la gráfica de la función en dicho punto. En dimensiones más elevadas, la derivada de una función en un punto es la transformación lineal que más se aproxima a la función en valores cercanos de ese punto. Algo estrechamente relacionado es el diferencial de una función.
El proceso de encontrar una derivada es llamado diferenciación. El teorema fundamental del cálculo dice que la diferenciación es el proceso inverso de la integración en funciones continuas.
funciones polinomiales de grado 2 y las particularidades de los modelos cuadráticos
ecuaciones cuadráticas pueden tomar tres formas útiles: La forma de vértice es y a(x h)2 k. Esta forma es útil para decir cómo lay x2 ha sido transformada. El vértice (h, k) de la parábola es ela dice la cantidad de estiramiento vertical,a revela una reflexión alrededor del eje x. La forma factorizada es y a(x x1)(x x2). De esta forma es fácil decir que lasx1 y x2 y que la gráfica tiene intersecciones x en x1 y x2. La forma general es y ax2 bx c. Esta forma es útil para hallar que lay es c—la parábola cruza el eje y en (0, c). Si la ecuación describe laa es la mitad de la aceleraciónb es la velocidad inicial y c es la altura inicial por encima
Las
●
gráfica madre
punto más alto o más bajo. El factor
y un valor negativo de
●
raíces de la ecuación son
●
intersección
altura de un objeto que sube o cae, entonces
debida a la gravedad,
del nivel del suelo
línea recta
la recta o línea recta, es el ente ideal que se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos puntos; está compuesta de infinitos segmentos (el fragmento de línea más corto que une dos puntos). También se describe como la sucesión continua e indefinida de puntos en una sola dimensión, o sea, no posee principio ni fin.
Es uno de los entes geométricos fundamentales, junto al punto y el plano. Son considerados conceptos apriorísticos ya que su definición sólo es posible a partir de la descripción de las características de otros elementos similares. Así, es posible elaborar definiciones basándose en los Postulados característicos que determinan relaciones entre los entes fundamentales. Las rectas se suelen denominar con una letra minúscula.
Las líneas rectas pueden ser expresadas mediante una ecuación del tipo y = m x + b, donde x, y son variables en un plano. En dicha expresión m es denominada la "pendiente de la recta" y está relacionada con la inclinación que toma la recta respecto a un par de ejes que definen el plano. Mientras que b es el denominado "término independiente" u "ordenada al origen" y es el valor del punto en el cual la recta corta al eje vertical en el plano.
Es uno de los entes geométricos fundamentales, junto al punto y el plano. Son considerados conceptos apriorísticos ya que su definición sólo es posible a partir de la descripción de las características de otros elementos similares. Así, es posible elaborar definiciones basándose en los Postulados característicos que determinan relaciones entre los entes fundamentales. Las rectas se suelen denominar con una letra minúscula.
Las líneas rectas pueden ser expresadas mediante una ecuación del tipo y = m x + b, donde x, y son variables en un plano. En dicha expresión m es denominada la "pendiente de la recta" y está relacionada con la inclinación que toma la recta respecto a un par de ejes que definen el plano. Mientras que b es el denominado "término independiente" u "ordenada al origen" y es el valor del punto en el cual la recta corta al eje vertical en el plano.
funciones polinomiales de grado
las funciones polinómicas son las funciones

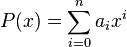

- donde
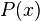 es un polinomio en
es un polinomio en  ,
, 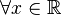 , es decir, una suma finita de potencias de
, es decir, una suma finita de potencias de  multiplicados por coeficientes reales, de la forma:
multiplicados por coeficientes reales, de la forma:
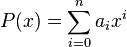
[editar] Funciones polinómicas básicas
Algunas funciones polinómicas reciben un nombre especial según el grado del polinomio:| Grado | Nombre | Expresión |
|---|---|---|
| 0 | función constante | y = a |
| 1 | función lineal | y = ax + b es un binomio del primer grado |
| 2 | función cuadrática | y = ax² + bx + c es un trinomio del segundo grado |
| 3 | función cúbica | y = ax³ + bx² + cx + d es un cuatrinomio de tercer grado |
Suscribirse a:
Entradas (Atom)